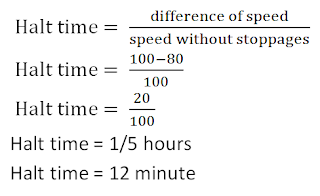Question 1.
If some distance is traveled at a speed of ‘x’ km/h and the same distance is traveled at a speed of ‘y’ km/h. Then, the average speed during the whole journey:


Example: If the distance between Goa to Delhi is 750 km. A person goes at a speed of 60 km/h and returns at a speed of 40 km/h. Find the average speed.
Solution:



Example: If the distance between Goa to Delhi is 750 km. A person goes at a speed of 60 km/h and returns at a speed of 40 km/h. Find the average speed.
Solution:


Question 2.
If the distance is different than average speed is:

Example: If the speed of the bus is 30 km/h for the 90 km and 35 km/h for the distance of 70 km. Find the average distance.
Solution:

Example: If the speed of the bus is 30 km/h for the 90 km and 35 km/h for the distance of 70 km. Find the average distance.
Solution:
If the speed ratio between P and Q is a:b, so to cover the same distance the ratio between times taken by them will be

Example: The ratio between the speed of two cars is 6:8. If the second car covers a certain distance in 9 hours, then find the time taken by the first car to cover the same distance.
Solution:


Example: The ratio between the speed of two cars is 6:8. If the second car covers a certain distance in 9 hours, then find the time taken by the first car to cover the same distance.
Solution:

Question 4.
To find the time of halts when the speed with stoppages is
a km/h and speed without stoppages b km/h:

Example:A man running on a road without any stoppage at an average speed of 100 km /hr, and he covers the same distance with stoppage at an average speed of 80 km/hr. How many minutes per hour does boy stop?
Solution:
a km/h and speed without stoppages b km/h:

Example:A man running on a road without any stoppage at an average speed of 100 km /hr, and he covers the same distance with stoppage at an average speed of 80 km/hr. How many minutes per hour does boy stop?
Solution:
Question 5.
A man walks at x/y speed of his actual speed reaches his destination z mint later. To cover this distance actual time is:


Example: Walking at 3/4th of usual speed, A person is late by 10 minutes. Find the usual time.
Solution:




Example: Walking at 3/4th of usual speed, A person is late by 10 minutes. Find the usual time.
Solution:


Question 6.
A man walks at x/y speed of his actual speed reaches his destination z mint early. To cover this distance actual time is:


Example: Walking at 6/5th of usual speed, A person reached early by 5 minutes. Find the usual time.
Solution:




Example: Walking at 6/5th of usual speed, A person reached early by 5 minutes. Find the usual time.
Solution:


Question 7.
A & B start moving towards each other at same time. After meeting each other, they reach their destinations after ‘a’ and ‘b’ hrs respectively.
A’s Speed: B’s Speed = √b: √a
Example: Two trains, one from Delhi to Pune and the other from Pune to Delhi, start simultaneously. After they meet, the trains reach their destinations after 4 hours and 9 hours respectively. What will be the ratio of their speeds?
Solution:
A:B = √b : √a
A:B = √9 : √4
A:B = 3:2
A’s Speed: B’s Speed = √b: √a
Example: Two trains, one from Delhi to Pune and the other from Pune to Delhi, start simultaneously. After they meet, the trains reach their destinations after 4 hours and 9 hours respectively. What will be the ratio of their speeds?
Solution:
A:B = √b : √a
A:B = √9 : √4
A:B = 3:2
Question 8.
A man/train leaves from A at x1 AM and reaches Q at x2 AM. Another man/train leaves from Q at y1 AM and reaches P at y2 PM. They will meet:

Example: A train leaves from Bombay at 6:30 AM and reaches Jaipur at 10:30 AM. Another train leaves from Jaipur at 9 AM and reaches Delhi at 12:30 PM. When they will meet?
Solution:
Example: A train leaves from Bombay at 6:30 AM and reaches Jaipur at 10:30 AM. Another train leaves from Jaipur at 9 AM and reaches Delhi at 12:30 PM. When they will meet?
Solution:
If the distance between A to B is D km. Two persons P and Q travel from points A to B, with the speed of 'a' and 'b' respectively and Q reaches B first, returns immediately and meets P at X, then
Distance traveled by P (from points A to X) =

Example: Suhail and Meetu travel from point A to B, a distance of 48 km, at 7 km/ h and 9 km/ h, respectively. Meetu reaches B first and returns immediately and meets Suhail at R. Find the distance from points A to R.
Solution:




Distance traveled by P (from points A to X) =


Example: Suhail and Meetu travel from point A to B, a distance of 48 km, at 7 km/ h and 9 km/ h, respectively. Meetu reaches B first and returns immediately and meets Suhail at R. Find the distance from points A to R.
Solution:




Question 10.
Relative Speed:
(i). If two objects are moving in the same direction with the speeds of a km/h and b km/h then their relative speed is |a‐b|.
(ii). If two objects are moving in opposite direction with the speeds of a km/h and b km/h then their relative speed is (a+b).
Example: 2 men A and B started from a place P walking at 4 km/h and 3 km/h respectively. How many km will they be a part at the end of 1 hour?
(i) If they walk in the same direction.
(ii) If they walk in opposite direction.
Solution:
(i): Relative speed = Ia-bI
= I 4-5 I
= 1 km/h
(i). If two objects are moving in the same direction with the speeds of a km/h and b km/h then their relative speed is |a‐b|.
(ii). If two objects are moving in opposite direction with the speeds of a km/h and b km/h then their relative speed is (a+b).
Example: 2 men A and B started from a place P walking at 4 km/h and 3 km/h respectively. How many km will they be a part at the end of 1 hour?
(i) If they walk in the same direction.
(ii) If they walk in opposite direction.
Solution:
(i): Relative speed = Ia-bI
= I 4-5 I
= 1 km/h
(ii): Relative speed = a+b
= 4+5
= 9 km/h
= 4+5
= 9 km/h